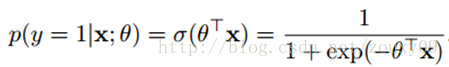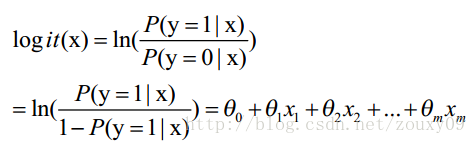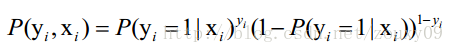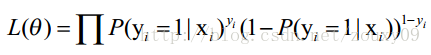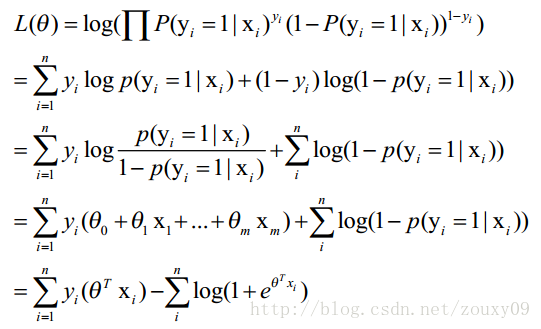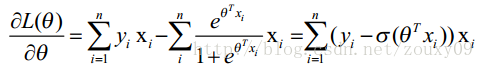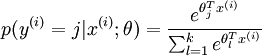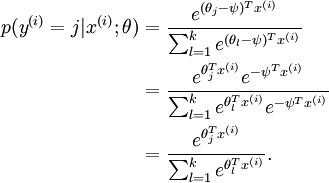判断学习速率是否合适？每步都下降即可。这篇先不整理吧...

　　这节学习的是逻辑回归（Logistic Regression），也算进入了比较正统的机器学习算法。啥叫正统呢？我概念里面机器学习算法一般是这样一个步骤：

　　1）对于一个问题，我们用数学语言来描述它，然后建立一个模型，例如回归模型或者分类模型等来描述这个问题；

　　2）通过最大似然、最大后验概率或者最小化分类误差等等建立模型的代价函数，也就是一个最优化问题。找到最优化问题的解，也就是能拟合我们的数据的最好的模型参数；

　　3）然后我们需要求解这个代价函数，找到最优解。这求解也就分很多种情况了：

      a）如果这个优化函数存在解析解。例如我们求最值一般是对代价函数求导，找到导数为0的点，也就是最大值或者最小值的地方了。如果代价函数能简单求导，并且求导后为0的式子存在解析解，那么我们就可以直接得到最优的参数了。

      b）如果式子很难求导，例如函数里面存在隐含的变量或者变量相互间存在耦合，也就互相依赖的情况。或者求导后式子得不到解释解，例如未知参数的个数大于已知方程组的个数等。这时候我们就需要借助迭代算法来一步一步找到最有解了。迭代是个很神奇的东西，它将远大的目标（也就是找到最优的解，例如爬上山顶）记在心上，然后给自己定个短期目标（也就是每走一步，就离远大的目标更近一点），脚踏实地，心无旁贷，像个蜗牛一样，一步一步往上爬，支撑它的唯一信念是：只要我每一步都爬高一点，那么积跬步，肯定能达到自己人生的巅峰，尽享山登绝顶我为峰的豪迈与忘我。

       另外需要考虑的情况是，如果代价函数是凸函数，那么就存在全局最优解，方圆五百里就只有一个山峰，那命中注定了，它就是你要找的唯一了。但如果是非凸的，那么就会有很多局部最优的解，有一望无际的山峰，人的视野是伟大的也是渺小的，你不知道哪个山峰才是最高的，可能你会被命运作弄，很无辜的陷入一个局部最优里面，坐井观天，以为自己找到的就是最好的。没想到山外有山，人外有人，光芒总在未知的远处默默绽放。但也许命运眷恋善良的你，带给你的总是最好的归宿。也有很多不信命的人，觉得人定胜天的人，誓要找到最好的，否则不会罢休，永不向命运妥协，除非自己有一天累了，倒下了，也要靠剩下的一口气，迈出一口气能支撑的路程。好悲凉啊……哈哈。

 直觉上，一个线性模型的输出值 y 越大，这个事件 P(Y=1|x) 发生的概率就越大。 另一方面，我们可以用事件的几率（odds）来表示事件发生与不发生的比值，假设发生的概率是 p ，那么发生的几率（odds）是 p/(1-p) ， odds 的值域是 0 到正无穷，几率越大，发生的可能性越大。将我们的直觉与几率联系起来的就是下面这个（log odds）或者是 logit 函数 (有点牵强 - -!)：

  进而可以求出概率 p 关于 w 点乘 x 的表示：

 这就是传说中的  了，以 w 点乘 x 为自变量，函数图像如下:

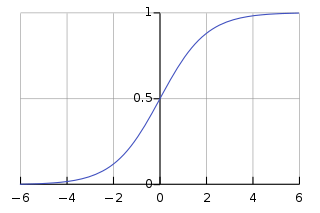
(注：从图中可以看到 wx 越大，p 值越高，在线性分类器中，一般 wx = 0 是分界面，对应了 logistic regression 中 p = 0.5)

一、逻辑回归（LogisticRegression）

       Logistic regression （逻辑回归）是当前业界比较常用的机器学习方法，用于估计某种事物的可能性。之前在经典之作《数学之美》中也看到了它用于广告预测，也就是根据某广告被用户点击的可能性，把最可能被用户点击的广告摆在用户能看到的地方，然后叫他“你点我啊！”用户点了，你就有钱收了。这就是为什么我们的电脑现在广告泛滥的原因了。

       还有类似的某用户购买某商品的可能性，某病人患有某种疾病的可能性啊等等。

　　Logistic regression可以用来回归，也可以用来分类，主要是二分类。还记得上几节讲的支持向量机SVM吗？它就是个二分类的例如，它可以将两个不同类别的样本给分开，思想是找到最能区分它们的那个分类超平面。但当你给一个新的样本给它，它能够给你的只有一个答案，你这个样本是正类还是负类。例如你问SVM，某个女生是否喜欢你，它只会回答你喜欢或者不喜欢。这对我们来说，显得太粗鲁了，要不希望，要不绝望，这都不利于身心健康。那如果它可以告诉我，她很喜欢、有一点喜欢、不怎么喜欢或者一点都不喜欢，你想都不用想了等等，告诉你她有49%的几率喜欢你，总比直接说她不喜欢你，来得温柔。而且还提供了额外的信息，她来到你的身边你有多少希望，你得再努力多少倍，知己知彼百战百胜，哈哈。Logistic regression就是这么温柔的，它给我们提供的就是你的这个样本属于正类的可能性是多少。

　　得来点数学。假设我们的样本是{

x, y}，y是0或者1，表示正类或者负类，x是我们的m维的样本特征向量。那么这个样本x属于正类，也就是y=1的“概率”可以通过下面的逻辑函数来表示：

       这里θ是模型参数，也就是回归系数，σ是sigmoid函数。实际上这个函数是由下面的对数几率（也就是x属于正类的可能性和负类的可能性的比值的对数）变换得到的：

       换句话说，y也就是我们关系的变量，例如她喜不喜欢你，与多个自变量（因素）有关，例如你人品怎样、车子是两个轮的还是四个轮的、长得胜过潘安还是和犀利哥有得一拼、有千尺豪宅还是三寸茅庐等等，我们把这些因素表示为x₁, x₂,…, x_m。那这个女的怎样考量这些因素呢？最快的方式就是把这些因素的得分都加起来，最后得到的和越大，就表示越喜欢。但每个人心里其实都有一杆称，每个人考虑的因素不同，萝卜青菜，各有所爱嘛。例如这个女生更看中你的人品，人品的权值是0.6，不看重你有没有钱，没钱了一起努力奋斗，那么有没有钱的权值是0.001等等。我们将这些对应x₁, x₂,…, x_m的权值叫做回归系数，表达为θ₁, θ₂,…, θ_m。他们的加权和就是你的总得分了。请选择你的心仪男生，非诚勿扰！哈哈。

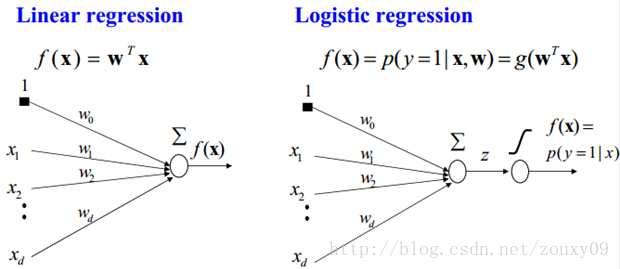
       所以说上面的logistic回归就是一个线性分类模型，它与线性回归的不同点在于：为了将线性回归输出的很大范围的数，例如从负无穷到正无穷，压缩到0和1之间，这样的输出值表达为“可能性”才能说服广大民众。当然了，把大值压缩到这个范围还有个很好的好处，就是可以消除特别冒尖的变量的影响（不知道理解的是否正确）。而实现这个伟大的功能其实就只需要平凡一举，也就是在输出加一个logistic函数。另外，对于二分类来说，可以简单的认为：如果样本x属于正类的概率大于0.5，那么就判定它是正类，否则就是负类。实际上，SVM的类概率就是样本到边界的距离，这个活实际上就让logistic regression给干了。

       所以说，LogisticRegression 就是一个被logistic方程归一化后的线性回归，仅此而已。

 

好了，关于LR的八卦就聊到这。归入到正统的机器学习框架下，模型选好了，只是模型的参数θ还是未知的，我们需要用我们收集到的数据来训练求解得到它。那我们下一步要做的事情就是建立代价函数了。

       LogisticRegression最基本的学习算法是最大似然。

 假设我们有n个独立的训练样本{(x₁, y₁) ,(x₂, y₂),…, (x_n, y_n)}，y={0, 1}。那每一个观察到的样本(x_i, y_i)出现的概率是：

       上面为什么是这样呢？当y=1的时候，后面那一项是不是没有了，那就只剩下x属于1类的概率，当y=0的时候，第一项是不是没有了，那就只剩下后面那个x属于0的概率（1减去x属于1的概率）。所以不管y是0还是1，上面得到的数，都是(x, y)出现的概率。那我们的整个样本集，也就是n个独立的样本出现的似然函数为（因为每个样本都是独立的，所以n个样本出现的概率就是他们各自出现的概率相乘）：

       那最大似然法就是求模型中使得似然函数最大的系数取值θ*。这个最大似然就是我们的代价函数（cost function）了。

       OK，那代价函数有了，我们下一步要做的就是优化求解了。我们先尝试对上面的代价函数求导，看导数为0的时候可不可以解出来，也就是有没有解析解，有这个解的时候，就皆大欢喜了，一步到位。如果没有就需要通过迭代了，耗时耗力。

       我们先变换下L(θ)：取自然对数，然后化简（不要看到一堆公式就害怕哦，很简单的哦，只需要耐心一点点，自己动手推推就知道了。注：有x_i的时候，表示它是第i个样本，下面没有做区分了，相信你的眼睛是雪亮的），得到：

       这时候，用L(θ)对θ求导，得到：

       然后我们令该导数为0，你会很失望的发现，它无法解析求解。不信你就去尝试一下。所以没办法了，只能借助高大上的迭代来搞定了。这里选用了经典的梯度下降算法。

  注：因为本文中是求解的Logit回归的代价函数是似然函数，需要最大化似然函数。所以我们要用的是梯度上升算法。但因为其和梯度下降的原理是一样的，只是一个是找最大值，一个是找最小值。找最大值的方向就是梯度的方向，最小值的方向就是梯度的负方向。不影响我们的说明。另外，最大似然可以通过取负对数，转化为求最小值

产生这个现象的原因是存在一些无法正确分类的样本点，也就是我们的数据集并非线性可分，但我们的logistic regression是线性分类模型，对非线性可分情况无能为力。然而我们的优化程序并没能意识到这些不正常的样本点，还一视同仁的对待，调整系数去减少对这些样本的分类误差，从而导致了在每次迭代时引发系数的剧烈改变。对我们来说，我们期待算法能避免来回波动，从而快速稳定和收敛到某个值。

       对随机梯度下降算法，我们做两处改进来避免上述的波动问题：

1）在每次迭代时，调整更新步长alpha的值。随着迭代的进行，alpha越来越小，这会缓解系数的高频波动（也就是每次迭代系数改变得太大，跳的跨度太大）。当然了，为了避免alpha随着迭代不断减小到接近于0（这时候，系数几乎没有调整，那么迭代也没有意义了），我们约束alpha一定大于一个稍微大点的常数项。

2）每次迭代，改变样本的优化顺序。也就是随机选择样本来更新回归系数。这样做可以减少周期性的波动，因为样本顺序的改变，使得每次迭代不再形成周期性。

 

 

 

 

 

 

 

 

 

 

1.从方差代价函数说起

代价函数经常用方差代价函数（即采用均方误差MSE），比如对于一个神经元（单输入单输出，sigmoid函数）,定义其代价函数为：

其中y是我们期望的输出，a为神经元的实际输出【 a=σ(z), where z=wx+b 】。

在训练神经网络过程中，我们通过梯度下降算法来更新w和b，因此需要计算代价函数对w和b的导数：

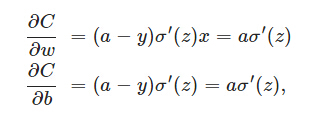
然后更新w、b：

w <—— w - η* ∂C/∂w = w - η * a *σ′(z)

b <—— b - η* ∂C/∂b = b - η * a * σ′(z)

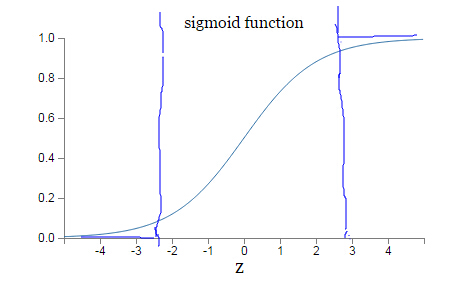
因为sigmoid函数的性质，导致σ′(z)在z取大部分值时会很小（如下图标出来的两端，几近于平坦），这样会使得w和b更新非常慢（因为η * a * σ′(z)这一项接近于0）。

 

 

2.交叉熵代价函数（cross-entropy cost function）

为了克服这个缺点，引入了交叉熵代价函数（下面的公式对应一个神经元，多输入单输出）：

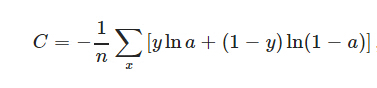
其中y为期望的输出，a为神经元实际输出【a=σ(z), where z=∑Wj*Xj+b】

与方差代价函数一样，交叉熵代价函数同样有两个性质：

• 非负性。（所以我们的目标就是最小化代价函数）
• 当真实输出a与期望输出y接近的时候，代价函数接近于0.(比如y=0，a～0；y=1，a~1时，代价函数都接近0)。

另外，它可以克服方差代价函数更新权重过慢的问题。我们同样看看它的导数：

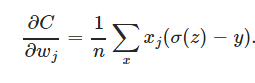
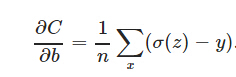
可以看到，导数中没有σ′(z)这一项，权重的更新是受σ(z)−y这一项影响，即受误差的影响。所以当误差大的时候，权重更新就快，当误差小的时候，权重的更新就慢。这是一个很好的性质。

3.总结

• 当我们用sigmoid函数作为神经元的激活函数时，最好使用交叉熵代价函数来替代方差代价函数，以避免训练过程太慢。

• 不过，你也许会问，为什么是交叉熵函数？导数中不带σ′(z)项的函数有无数种，怎么就想到用交叉熵函数？这自然是有来头的，更深入的讨论就不写了，少年请自行了解。

• 另外，交叉熵函数的形式是−[ylna+(1−y)ln(1−a)]而不是 −[alny+(1−a)ln(1−y)]，为什么？因为当期望输出的y=0时，lny没有意义；当期望y=1时，ln(1-y)没有意义。而因为a是sigmoid函数的实际输出，永远不会等于0或1，只会无限接近于0或者1，因此不存在这个问题。

 

logistic regression 在多类上的推广又叫 softmax regression， 在数字手写识别中，我们要识别的是十个类别，每次从输入层输入 28×28 个像素，输出层就可以得到本次输入可能为 0, 1, 2… 的概率。

在 softmax regression 中，输入的样本属于第 j 类的概率可以写成：

  (注：对比第一部分提到过的中间一步，有什么不同？)   

     注意到，这个回归的参数向量减去一个常数向量，会有什么结果：

  没有变化！这说明如果某一个向量是代价函数的极小值点，那么这个向量在减去一个任意的常数向量也是极小值点，这是因为 softmax 模型被过度参数化了。(题外话：回想一下在线性模型中，同时将 w 和 b 扩大两倍，模型的分界线没有变化，但是模型的输出可信度却增大了两倍，而在训练迭代中， w 和 b 绝对值越来越大，所以 SVM 中就有了函数距离和几何距离的概念)

  既然模型被过度参数化了，我们就事先确定一个参数，比如将 w1 替换成全零向量，将 w1.x = 0 带入 binomial softmax regression ，得到了我们最开始的二项 logistic regression (可以动手算一算), 用图就可以表示为

  (注：虚线表示为 0 的权重，在第一张图中没有画出来，可以看到 logistic regression 就是 softmax regression 的一种特殊情况)。

实际应用中，为了使算法实现更简单清楚，往往保留所有参数，而不任意地将某一参数设置为 0。我们可以对代价函数做一个改动：加入权重衰减 (weight decay)。 权重衰减可以解决 softmax 回归的参数冗余所带来的数值问题。并且此时代价函数变成了严格的凸函数， Hessian矩阵变为可逆矩阵，保证有唯一的解。(感觉与线性分类器里限制 ||w|| 或者设置某一个 w 为全零向量一样起到了减参的作用，但是这个计算起来简单清晰，可以用高斯分布的 MAP 来推导，其结果是将 w 软性地限制在超球空间，有一点 “soft” 的味道，个人理解^ ^)

  加入权重衰减后的代价函数是：

  等号右边第一项是训练样本 label 对应的输出节点上的概率的负对数，第二项是 weight decay ，可以使用梯度下降法和 L-BFGS 等算法可以保证收敛到全局最优解。总结起来，logistic regression 是 softmax regression 的一种特殊形式，前者是二类问题，后者是多类问题，前者的非线性函数的唯一确定的 sigmoid function (默认 label 为 0 的权重为全零向量的推导结果), 后者是 softmax, 有时候我们并不特意把它们区分开来。

 

第一部分：Logistic Regression

 

/*************（一）~（二）、Classification / Hypothesis Representation***********/

假设随Tumor Size变化，预测病人的肿瘤是恶性（malignant）还是良性（benign）的情况。

给出8个数据如下：

   

 

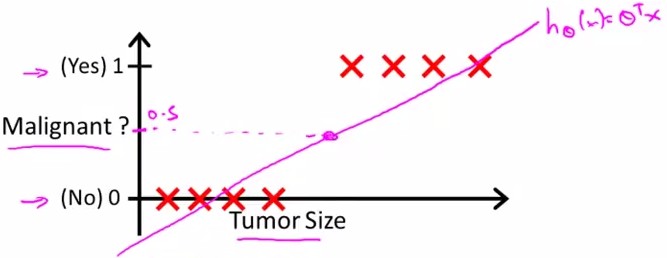
假设进行linear regression得到的hypothesis线性方程如上图中粉线所示，则可以确定一个threshold:0.5进行predict

y=1, if h(x)>=0.5

y=0, if  h(x)<0.5

即malignant=0.5的点投影下来，其右边的点预测y=1;左边预测y=0；则能够很好地进行分类。

那么，如果数据集是这样的呢？

这种情况下，假设linear regression预测为蓝线，那么由0.5的boundary得到的线性方程中，不能很好地进行分类。因为不满足

 

y=1, h(x)>0.5

y=0, h(x)<=0.5

这时，我们引入logistic regression model：

所谓Sigmoid function或Logistic function就是这样一个函数g(z)见上图所示

当z>=0时，g(z)>=0.5；当z<0时，g(z)<0.5

由下图中公式知，给定了数据x和参数θ，y=0和y=1的概率和=1

 

 

 

 

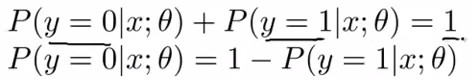
/*****************************（三）、decision boundary**************************/

所谓Decision Boundary就是能够将所有数据点进行很好地分类的h(x)边界。

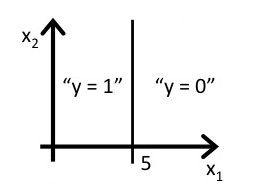
如下图所示，假设形如h(x)=g(θ0+θ1x1+θ2x2)的hypothesis参数θ=[-3,1,1]T, 则有

predict Y=1, if -3+x1+x2>=0

predict Y=0, if -3+x1+x2<0

刚好能够将图中所示数据集进行很好地分类

Another Example:

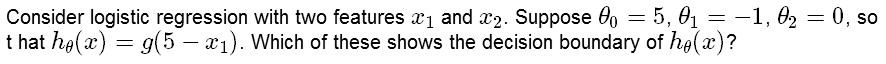
answer:

除了线性boundary还有非线性decision boundaries，比如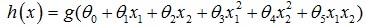

下图中，进行分类的decision boundary就是一个半径为1的圆，如图所示：

 

 

 

该部分讲述简化的logistic regression系统中how to implement gradient descents for logistic regression.

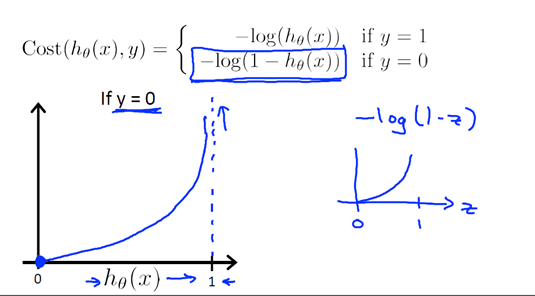
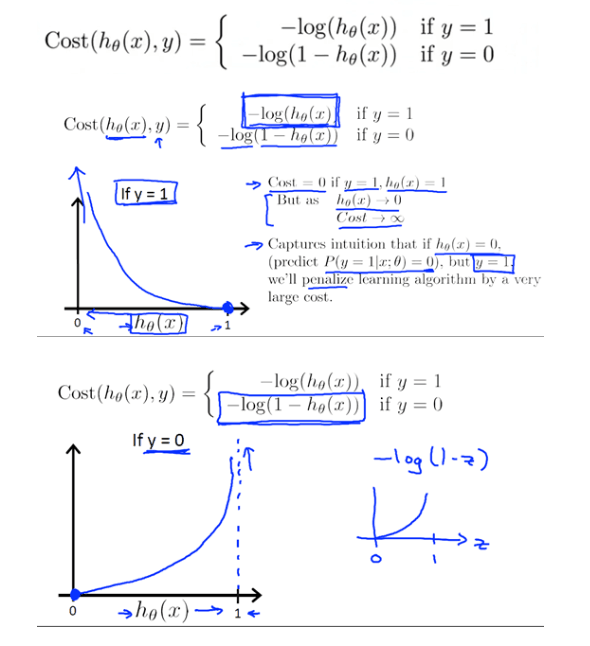
假设我们的数据点中y只会取0和1, 对于一个logistic regression model系统，有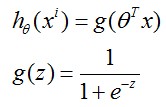，那么cost function定义如下：

由于y只会取0,1，那么就可以写成

 

成

不信的话可以把y=0,y=1分别代入，可以发现这个J（θ）和上面的Cost(hθ(x),y)是一样的(*^__^*) ，那么剩下的工作就是求能最小化 J(θ)的θ了~

 

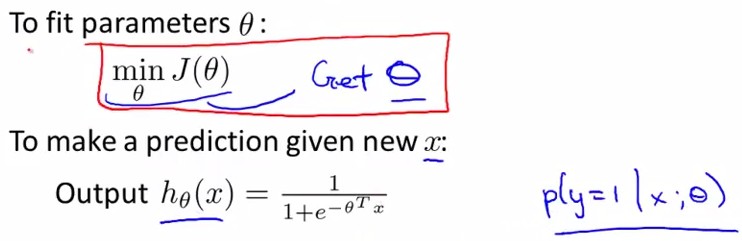
在中我们已经讲了如何应用Gradient Descent, 也就是下图Repeat中的部分，将θ中所有维同时进行更新，而J(θ)的导数可以由下面的式子求得，结果如下图手写所示：

现在将其带入Repeat中

：

这是我们惊奇的发现，它和第一章中我们得到的公式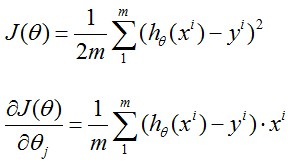是一样滴~

也就是说，下图中所示，不管h(x)的表达式是线性的还是logistic regression model, 都能得到如下的参数更新过程。

 

比如我想分成K类，那么就将其中一类作为positive，另（k-1）合起来作为negative，这样进行K个h(θ)的参数优化，每次得到的一个hθ(x)是指给定θ和x，它属于positive的类的概率。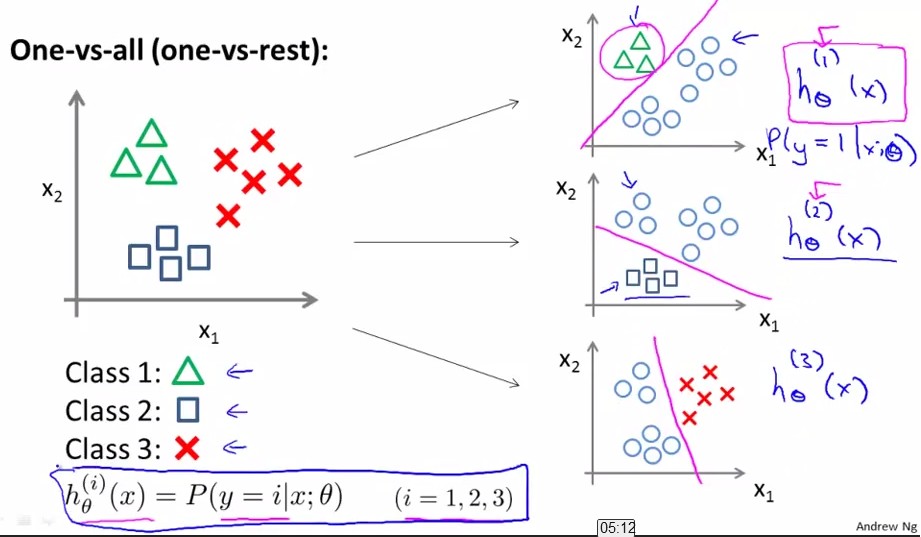

 

按照上面这种方法，给定一个输入向量x，获得最大hθ(x)的类就是x所分到的类。

 

 

 

 

 

 

The Problem of overfitting:

overfitting就是过拟合，如下图中最右边的那幅图。对于以上讲述的两类（logistic regression和linear regression）都有overfitting的问题，下面分别用两幅图进行解释：

 

<Linear Regression>:

 

 

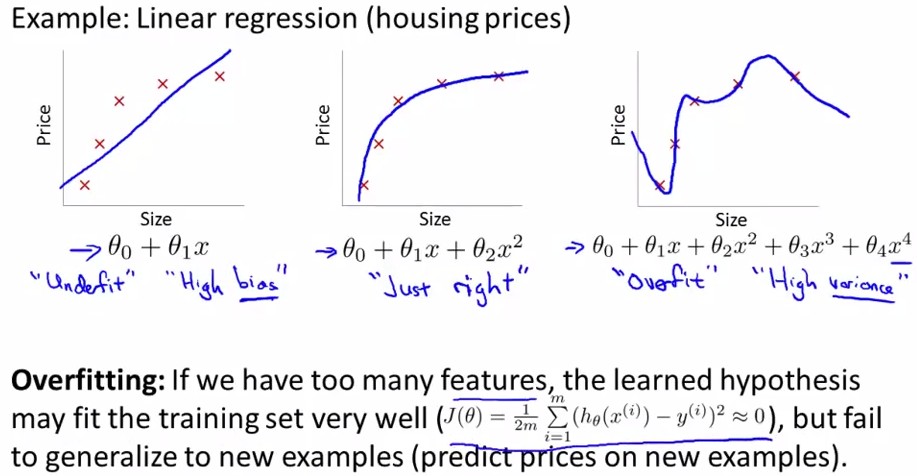
<logistic regression>:

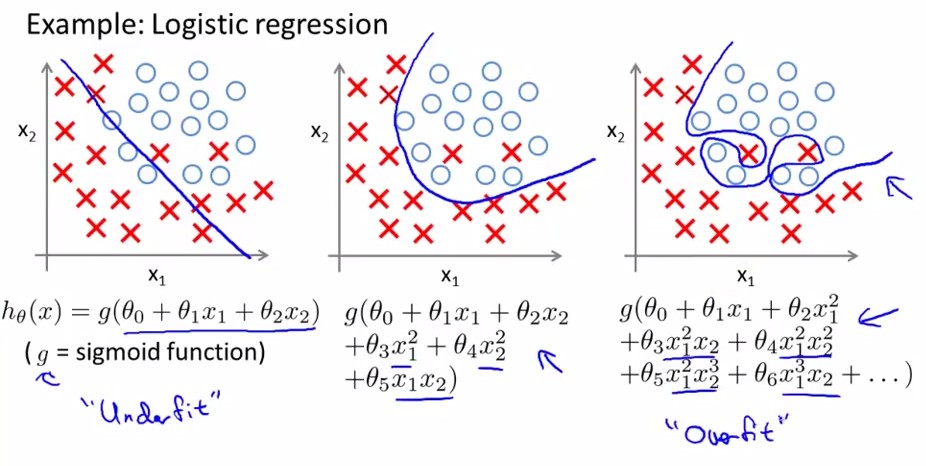
怎样解决过拟合问题呢？两个方法：

1. 减少feature个数（人工定义留多少个feature、算法选取这些feature）

2. 规格化（留下所有的feature，但对于部分feature定义其parameter非常小）

 

对于linear regression model, 我们的问题是最小化

写作矩阵表示即

i.e. the loss function can be written as

there we can get:

After regularization, however,we have:

 

对于Regularization，方法如下，定义cost function中θ3，θ4的parameter非常大，那么最小化cost function后就有非常小的θ3,θ4了。

 

写作公式如下，在cost function中加入θ1~θn的惩罚项：

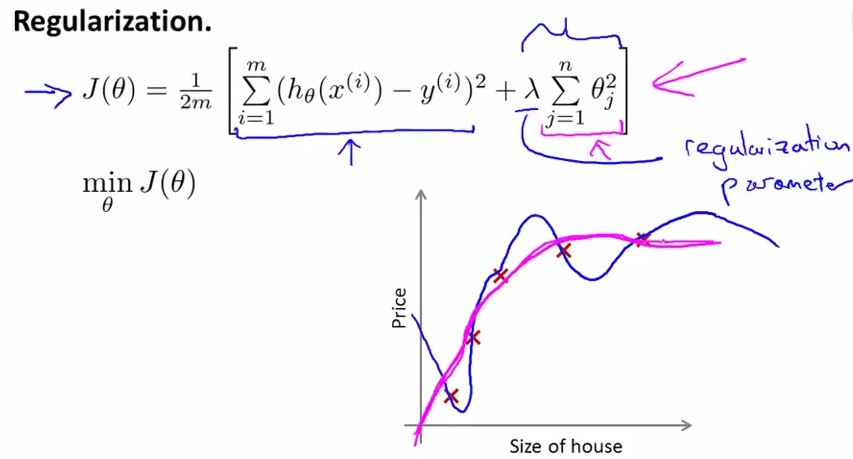
这里要注意λ的设置，见下面这个题目：

Q:

    A:λ很大会导致所有θ≈0

<Linear regression>:

首先看一下，按照上面的cost function的公式，如何应用gradient descent进行参数更新。

对于θ0，没有惩罚项，更新公式跟原来一样

对于其他θj，J(θ)对其求导后还要加上一项(λ/m)*θj，见下图：

如果不使用梯度下降法（gradient descent+regularization），而是用矩阵计算（normal equation）来求θ，也就求使J(θ)min的θ，令J(θ)对θj求导的所有导数等于0，有公式如下

 

如果不使用梯度下降法（gradient descent+regularization），而是用矩阵计算（normal equation）来求θ，也就求使J(θ)min的θ，令J(θ)对θj求导的所有导数等于0，有公式如下：

而且已经证明，上面公式中括号内的东西是可逆的。

<Logistic regression>:

前面已经讲过Logisitic Regression的cost function和overfitting的情况，如下图中所示:

和linear regression一样，我们给J(θ)加入关于θ的惩罚项来抑制过拟合：

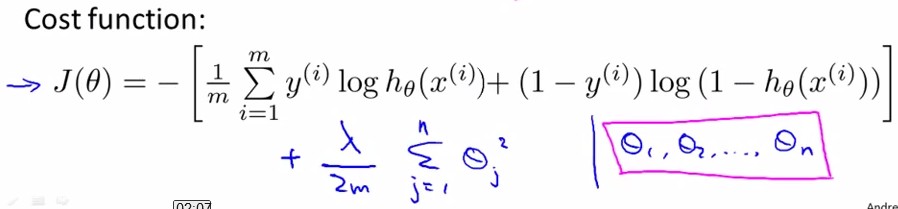
用Gradient Descent的方法，令J(θ)对θj求导都等于0，得到

这里我们发现，其实和线性回归的θ更新方法是一样的。